Question

An ultra-low friction pulley deal is as shown. The two weights experience an acceleration of 3.8m/s2. The first weight has 1.08kg. Find the mass of the second weight

Answer 1

The mass of the second weight is approximately 0.477 kg

Step-by-step explanation:

The given parameters are;

The acceleration experienced by the two weights = 3.8 m/s²

The mass of the first weight = 1.08 kg

The formula for the acceleration, a, of weights attached to a friction pulley, is given as follows;

`a = (g \cdot (M - m))/(M + m)`

Where;

a = The common acceleration of the two weights

g = The acceleration due to gravity = 9.81 m/s²

M = The mass of the first weight = 1.08 kg

m = The mass of the second weight

Therefore, we have;

`m = (M\cdot (g -a ))/(g + a) = (1.08* (9.81 -3.8 ))/(9.81 + 3.8) \approx 0.477`

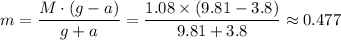
The mass of the second weight = m ≈ 0.477 kg

The mass of the second weight ≈ 0.477 kg.