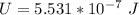Answer:
a
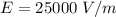
b

c
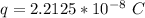
d
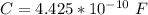
e
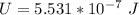
Step-by-step explanation:
From the question we are told that
The distance of separation is
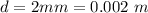
The voltage is
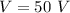
The area is
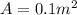
Generally the electric field is mathematically represented as
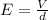
=>
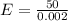
=>
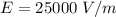
Generally the capacitance mathematically represented is
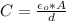
Here
 is the permitivity of free space with value
is the permitivity of free space with value
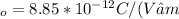
=>
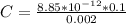
=>
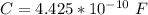
Generally the charge is mathematically represented as
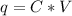
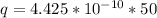
=>
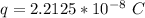
Generally the charge density is mathematically represented as

=>
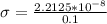
=>

Generally the energy stored in this capacitor is mathematically
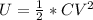
=>

=>