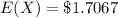Question

A bakery sells rolls in units of a dozen. The demand X (in 1000 units) for rolls has a gamma distribution with parameters α = 3, θ = 0.5, where θ is in units of days per 1000 units of rolls. It costs $ 2 to make a unit that sells for $ 5 on the first day when the rolls are fresh. Any leftover units are sold on the second day for $ 1. How many units should be made to maximize the expected value of the profit?

Answer 1

The value is
`E(X) =  \$ 1.7067`

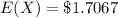
Explanation:

From the question we are told that

The parameters are α = 3, θ = 0.5

The cost of making a unit on the first day is c = $2

The selling price of a unit on the first day is s = $5

The selling price of a leftover unit on the second day is v = $ 1

Generally the profit of a unit on the first day is

`p_1 = 5 - 2`

`p_1 = \$3`

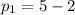
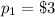
The profit of a unit on the second day is

`p_2 = 1 - 2`

=>
`p_2 = - \$1`

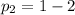
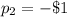
Generally the probability of making profit greater than $ 1 is mathematically represented as

`P(X >  1 ) = Gamma (X ,\alpha , \theta)`

=>
`P(X >  1 ) = Gamma (1 ,3 , 0.5)`

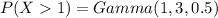
Now from the gamma distribution table we have that

`P(X >  1 ) =  0.67668`

Generally the probability of making profit less than or equal to $ 1 is mathematically represented as

`P(X \le  1 ) = 1 - P(X >  1 )`

=>
`P(X \le  1 ) = 1 - 0.67668`

=>
`P(X \le  1 ) = 0.32332`

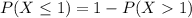
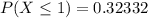
So the probability of making $3 is
`P(X >  1 ) =  0.67668`

and the probability of making -$1 is
`P(X \le  1 ) = 0.32332`

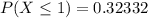
Generally the value of profit per day is mathematically represented as

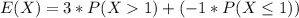
`E(X) =  3 *  P(X >  1 )   +   (-1  *  P(X \le 1 ) )`

=>
`E(X) =  3 * 0.67668   +   (-1  *  0.32332 )`

=>
`E(X) =  \$ 1.7067`