Question

Beverly is making peanut butter-banana bread. She always doubles the amount of nuts and peanut butter chips. The total amount of chips and nuts after doubling is 4 1/2 cups. The recipe says one and a half cups of peanut butter chips, an unknown number of cups of nuts, and three very ripe bananas. Write and solve an equation to find the original amount of nuts, x, in the recipe.

Answer 1

0.75 or three-fourth of a cup of nuts.

Explanation:

Given that:

Original recipe has

1. One and half cups of peanut butter

2. Unknown number of cups of nuts, let this amount be
`x` cups.

3. Three very ripe bananas.

Total amount of chips and nuts after doubling =
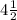`4(1)/(2)` cups

Before doubling, total amount of chips and nuts =
`4(1)/(2) / 2 = 2.25`

Now, as per given question statement:

`2.25=x+1.5`

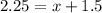
Subtracting the number 1.5 from both the sides to find the value of
`x`:

`2.25-1.5=x\\\Rightarrow x = \bold{0.75}`

Therefore, 0.75 or three-fourth of a cup of nuts is the original amount in the recipe.