Question

A paint company claims their paint will be completely dry within 45 minutes after application. Recently, customers have complained drying times are longer than the claimed 45 minutes. A consumer advocate group takes a random sample of 25 paint specimens and records their drying times. The average drying time x is 52. Consider dryng time, for all test specimens, to be normally distributed with ? = 6.

Suppose the claimed drying time is true, that is ? = 45 minutes, what is the probability of observing a sample mean of x = 52 or greater from a sample size of 25? (Round your answer to four decimal places.)

Answer 1

the probability of observing a sample mean of x = 52 or greater from a sample size of 25 is 0.0000026

Explanation:

Answer 2

The probability of observing a sample mean of x = 52 or greater from a sample size of 25 is 0.0000026

Explanation:

Mean =
`\mu = 45`

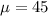
Population standard deviation =
`\sigma = 6`

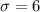
Sample size = n =25

Sample mean =
`\bar{x} = 52`

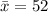
We are supposed to find the probability of observing a sample mean of x = 52 or greater from a sample size of 25 i.e.
`P(x\geq 52)`

`Z=(x-\mu)/((\sigma)/(√(n)))\\Z=(52-45)/((6)/(√(25)))`

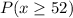
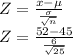
Z=5.83

P(Z<52)=0.9999974

`P(Z\geq 52)=1-P(z<52)=1-0.9999974=0.0000026`

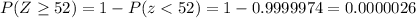
Hence the probability of observing a sample mean of x = 52 or greater from a sample size of 25 is 0.0000026