Question

A country’s population in 1991 Was 211 million in 1998 it was 215 million estimate the population in 2012 using the exponential growth formula

Answer 1

The population in 2012 is estimated in approximately 223 million people

Explanation:

Exponential Growth

The formula for exponential growth of a variable P at the growth rate r, as time t goes on in discrete intervals, or at integer times 0, 1, 2, 3, ..., is :

`\displaystyle P(t)=P_0(1+r)^(t)`

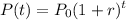
Where Po is the value of P at time 0.

The country’s population in 1991 was 211 million, and in 1998 it was 215 million. We have two discrete times to define the equation and set the year 1991 as t=0. Thus, the year 1998 is t=7.

The preliminary equation is:

`\displaystyle P(t)=211(1+r)^(t)`

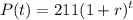
To find the value of 1+r, we use the second point (7,215):

`\displaystyle 215=211(1+r)^(7)`

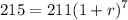
Dividing by 211:

`\displaystyle (215)/(211)=(1+r)^(7)`

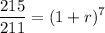
Solving:

`\displaystyle (1+r)=\sqrt[7]{(215)/(211)}`

Calculating:

`(1+r)=1.002686`

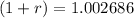
The complete equation is:

`\displaystyle P(t)=211(1.002686)^(t)`

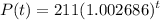
Estimate the population in 2012 (t=21):

`\displaystyle P(21)=211(1.002686)^(21)`

`P(21)\approx 223`

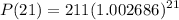
The population in 2012 is estimated in approximately 223 million people