Step (1)
We know that the sum of all the terms in an infinite geometric sequence finding from following equation whenever |q| < 1 .
q = magnitude
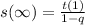
So :
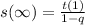
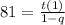
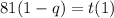
Remember it I'll use it again.
_________________________________
Step (2)
We know that the sum of the n first terms of a geometric sequence finding from following equation.
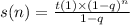
_________________________________
Sum of all terms starting from the third is 9.
So :
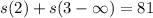
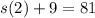
Sides minus 9
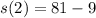
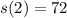
So :
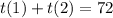
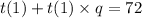
Factoring t(1)
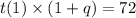
We have found t(1) = 81 ( 1 - q ) in step (1).
So :
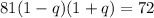
Divided sides by 81
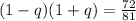
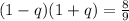
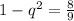
Subtract sides minus -1
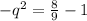
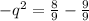
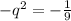
Negatives simplifies
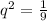
Radical sides
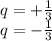
_________________________________
Step (4)
If q = 1/3 :
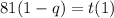
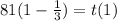
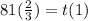
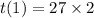
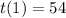
So :
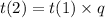
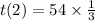
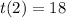
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
If q = - 1/3 :
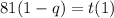
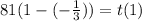
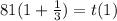
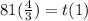
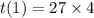
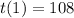
So :
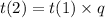
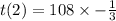
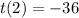
_________________________________
And we're done.
Thanks for watching buddy good luck.
♥️♥️♥️♥️♥️