Question

A circle is centered at the point O (0,0) and has a radius of the square root of 38?

Where’s does the K (6,1) lie?

Answer 1

The point (6,1) lies inside the circle.

Explanation:

Equation of a Circle

A circle centered at the point (h,k) and with radius r, can be expressed with the equation:

`(x-h)^2+(y-k)^2=r^2`

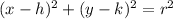
The center of the given circle is (0,0) and the radius is
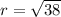`r=√(38)`, thus the equation of the circle is:

`(x-0)^2+(y-0)^2=(√(38))^2`

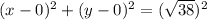
Simplifying:

`x^2+y^2=38`

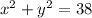
Each point (x,y) meeting the condition of the equation lies exactly on its circumference. For example, the point
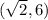`(√(2),6)` belongs to the circumference, but the origin (0,0) is inside the circle, and the point (5,5) is outside the circle.

We can tell the difference by evaluating the equation at each point. For the first point
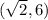`(√(2),6)`, the equation is:

`(√(2))^2+6^2=2+36=38`

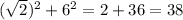
The equation is satisfied.

For the origin (0,0):

`0^2+0^2=0`

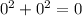
For the point (5,5):

`5^2+5^2=50`

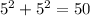
We can conclude that if the left side is greater than 38, the point is outside the circle, if it's less than 38, the point is inside the circle.

Let's test the point (6,1):

`6^2+1^2=37`

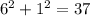
The point (6,1) lies inside the circle.