Question

A small truck has a mass of 2145 kg. How much work is required to decrease the speed of the vehicle from 25.0 m/s to 12.0 m/s on a level road?

Answer 1

To calculate the work required to decrease the speed of the truck, we use the work-energy principle. The work done is equal to the change in kinetic energy. Using the given values, the work required is -252,337.5 J.

Step-by-step explanation:

To calculate the work required to decrease the speed of the truck, we need to use the work-energy principle. The work done on an object is equal to the change in its kinetic energy. First, we need to find the initial and final kinetic energy of the truck.

The initial kinetic energy is given by KE1 = (1/2)mv12, where m is the mass of the truck and v1 is the initial velocity. The final kinetic energy is given by KE2 = (1/2)mv22, where v2 is the final velocity.

The work done is then equal to the difference in kinetic energy, W = KE2 - KE1. Substituting the given values, we have:

W = (1/2)(2145 kg)(12.0 m/s)2 - (1/2)(2145 kg)(25.0 m/s)2

W = -252,337.5 J

Answer 2

The work required is -515,872.5 J

Step-by-step explanation:

Work is defined in physics as the force that is applied to a body to move it from one point to another.

The total work W done on an object to move from one position A to another B is equal to the change in the kinetic energy of the object. That is, work is also defined as the change in the kinetic energy of an object.

Kinetic energy (Ec) depends on the mass and speed of the body. This energy is calculated by the expression:

`Ec=(1)/(2) *m*v^(2)`

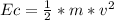
where kinetic energy is measured in Joules (J), mass in kilograms (kg), and velocity in meters per second (m/s).

The work (W) of this force is equal to the difference between the final value and the initial value of the kinetic energy of the particle:

`W=(1)/(2) *m*v2^(2)-(1)/(2) *m*v1^(2)`

`W=(1)/(2) *m*(v2^(2)-v1^(2))`

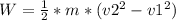
In this case:

• W=?
• m= 2,145 kg
• v2= 12
  `(m)/(s)`

• v1= 25
  `(m)/(s)`

Replacing:

`W=(1)/(2) *2145 kg*((12(m)/(s) )^(2)-(25(m)/(s) )^(2))`

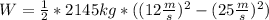
W= -515,872.5 J

The work required is -515,872.5 J