Question

Records on a fleet of trucks reveal that the average life of a set of spark plugs is normally distributed with a mean of 22,100 miles. A manufacturer of spark plugs claims that its plugs have an average life in excess of 22,100 miles. The fleet owner purchased 18 sets and found that the sample average life was 23,400 miles, the sample standard deviation was 1,500 miles and the computed test statistic was 3.677. Based on these findings, there is enough evidence to accept the manufacturer's claim at the 0.05 level.

Answer 1

There no sufficient evidence to support the manufactures claim at the 0.05 level

Explanation:

From the question we are told that

The mean is
`\mu = 22100 \ miles`

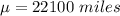
The sample mean is
`\= x = 23400 \ miles`

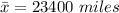
The sample size is
`n  = 18`

The standard deviation is
`\sigma  =  1 500 miles`

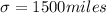
The test statistics is
`t = 3.677`

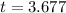
The level of significance is
`\alpha  =  0.05`

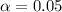
The null hypothesis is
`H_o :  \mu =  22100`

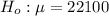
The alternative hypothesis is
`H_a :  \mu  \\e 22100`

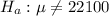
Generally the p-value is mathematically represented as

`p-value  =  2 *  P(t >3.677 )`

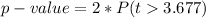
From the z-table
`P(t >3.677 )  =  0.000118`

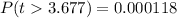
So

`p-value  =  2 *  0.000118`

=>
`p-value  =  0.000236`

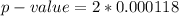
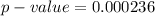
From he value given and obtained we see that
`p-value  <  \alpha`

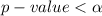
Hence we reject the null hypothesis

Hence there no sufficient evidence to support the manufactures claim