Question

Consider a cylinder of a gasoline engine at the beginning of the compression cycle, during which a fuel/air mixture (for our purposes mostly composed of nitrogen and oxygen, i.e. an ideal gas of diatomic molecules) at 300 K and 1 bar is compressed down to one-tenth volume (compression ratio of 10:1). Assume that the compression is rapid so no heat exchange occurs with the environment. Calculate the pressure and the temperature of the compressed gas. In a diesel engine the compression ratios are typically much higher; redo the same calculation with the compression ratio of 20:1.

Answer 1

(i) Final pressure and temperature are 25.119 bar and 753.566 K, (ii) Final pressure and temperature are 66.289 bar and 994.336 K.

Step-by-step explanation:

This system experiments an adiabatic compression, as such compression happens with no heat interaction between the piston-cylinder device and surroundings. This is a particular case of polytropic process, in which there is no entropy generation according to the Second Law of Thermodynamics.

The compression process is represented by the following formulas:

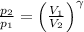`(p_(2))/(p_(1)) = \left((V_(1))/(V_(2)) \right) ^(\gamma)` (Eq. 1)

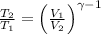`(T_(2))/(T_(1)) = \left((V_(1))/(V_(2)) \right)^(\gamma - 1)` (Eq. 2)

Where:

`p_(1)`,
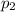`p_(2)` - Initial and final pressures, measured in bar.

`T_(1)`,
`T_(2)` - Initial and final temperatures, measured in Kelvins.

`V_(1)`,
`V_(2)` - Initial and final volumes, measured in cubic meters.

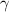`\gamma` - Specific heat ratio of air, dimensionless.

From Theory of Diesel and Otto Cycles we know that compression ratio is defined as:

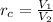`r_(c) = (V_(1))/(V_(2))` (Eq. 3)

And (Eqs. 1, 2) can be rewritten as follows:

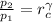`(p_(2))/(p_(1)) = r_(c)^(\gamma)` (Eq. 1b)

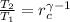`(T_(2))/(T_(1)) = r_(c)^(\gamma - 1)` (Eq. 2b)

Then, we clear final pressure and pressure in each expression and calculate them for each case:

`p_(2) = p_(1)\cdot r_(c)^(\gamma)`

`T_(2) = T_(1)\cdot r_(c)^(\gamma-1)`

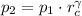
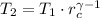
(i)
`r_(c) = 10`,
`p_(1) = 1\,bar`,
`T_(1) = 300\,K`,
`\gamma = 1.4`

`p_(2) = (1\,bar)\cdot 10^(1.4)`

`p_(2) = 25.119\,bar`

`T_(2) = (300\,K)\cdot 10^(0.4)`

`T_(2) = 753.566\,K`

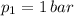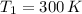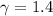
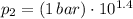
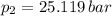
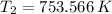
Final pressure and temperature are 25.119 bar and 753.566 K.

(ii)
`r_(c) = 20`,
`p_(1) = 1\,bar`,
`T_(1) = 300\,K`,
`\gamma = 1.4`

`p_(2) = (1\,bar)\cdot 20^(1.4)`

`p_(2) = 66.289\,bar`

`T_(2) = (300\,K)\cdot 20^(0.4)`

`T_(2) = 994.336\,K`

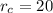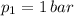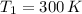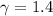
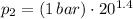
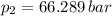
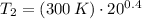
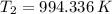
Final pressure and temperature are 66.289 bar and 994.336 K.