Question

Please help me with the domain and range of the graphs.?part 5​

Answer 1

Problem 5

Domain =
`-4 \le x \le 3`

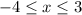
This is because the smallest x value allowed is x = -4 as shown by the left-most point. The right most point has x coordinate x = 3, so this is the largest value in the domain.

The domain in interval notation is [-4, 3]. The square brackets include the endpoint.

--------------

Range =
`-4 \le y \le 5`

We're now looking at the possible y values. The lowest point happens when y = -4 and the highest point is when y = 5. We can have any y value between those endpoints.

The range in interval notation is [-4, 5]

=============================================================

Problem 6

Domain =
`-2 \le x < 2`

Same idea as the previous problem. This time the left most point has x = -2 and the right most point has x coordinate x = 2.

The big difference here is that the open hole says to not include the endpoint. The domain in interval notation is [-2, 2) where we use a parenthesis to not include the endpoint.

-------------

Range =
`-4 \le y < 4`

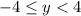
The smallest possible y value is y = -4. The ceiling for the y values is y = 4, but we can't actually reach this value due to the open hole.

The range in interval notation is [-4, 4)

=============================================================

Problem 7

Domain =
`-4 < x \le 2`

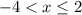
Same idea as earlier. Now the open hole is at the left endpoint. The right most point occurs not at an endpoint this time.

The domain in interval notation is (-4, 2]

-------------

Range:
`-4 < y < 4`

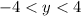
Both endpoints are open holes, so we exclude both endpoints.

The range in interval notation is (-4, 4). Unfortunately in this case, interval notation looks identical to ordered pair notation.

=============================================================

Problem 8

Domain =
`-5 < x < 3`

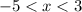
Domain in interval notation = (-5, 3)

The graph is too blurry to be able to determine the range.