Given:
A rectangle has a length 5 meters more than five times the width.
The area of the rectangle is less than 100 meters squared.
To find:
The expression or inequality that represents all possible widths of the rectangle.
Solution:
Let x be the width of the rectangle.
Length of the rectangle is 5 meters more than five times the width.
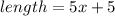
Area of rectangle is

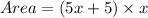
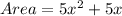
The area of the rectangle is less than 100 meters squared.


Divide both sides by 5.

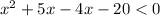
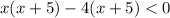
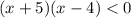
It is true if one factor is negative and other is positive. So,
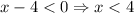 ...(i)
...(i)
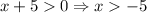 ...(ii)
...(ii)
Using (i) and (ii), we get
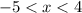
Therefore, the required expression or inequality for possible
widths of the rectangle is
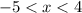 .
.