Question

Write the function in vertex form. y=x^2+5x-9

Answer 1

The function in the vertex form is y = (x + 2.5)² - 15.25

Explanation:

The vertex form of the quadratic function y = ax² + bx + c is:

y = a(x - h)² + k, where

• a is the coefficient of x²

• h, k are the coordinates of its vertex point

• h =
  `(-b)/(2a)`

• k equals y at x = h

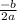
∵ The given function is y = x² + 5x - 9

∴ a = 1, b = 5, c = -9

→ Use a and b to find h

∵ h =
`(-b)/(2a)`

∴ h =
`(-5)/(2(1))=-2.5`

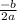
∴ h = -2.5

→ Find y at x = -2.5

∵ y = (-2.5)² + 5(-2.5) - 9 = 6.25 - 12.5 - 9

∴ y = -15.25

∴ k = -15.25

→ Substitute a, h, k in the vertex form above

∴ y = 1(x - -2.5)² + -15.25

∴ y = (x + 2.5)² - 15.25

The function in the vertex form is y = (x + 2.5)² - 15.25