Answer:
C) Se requiere 21.599 metros de malla para cercar el terreno.
D) El jardín de Gregorio tiene un área de 18.505 metros cuadrados.
Step-by-step explanation:
C) Por Geometría sabemos que el perímetro de una figura geométrica es la suma de todos sus lados, que en el caso del triángulo queda representado por:
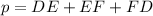 (Eq. 1)
(Eq. 1)
Donde:
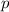 - Perímetro del triángulo, medido en metros.
- Perímetro del triángulo, medido en metros.
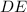 ,
,
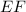 ,
,
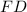 - Lados del triángulo, medidos en metros.
- Lados del triángulo, medidos en metros.
Ahora, podemos ampliar la ecuación al utilizar la fórmula de longitud de una línea, procedente de la Geometría Analítica. Calculamos la longitud de cada lado:
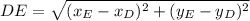 (Eq. 2)
(Eq. 2)
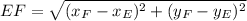 (Eq. 3)
(Eq. 3)
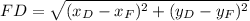 (Eq. 4)
(Eq. 4)
Si sabemos que
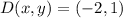 ,
,
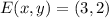 y
y
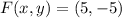 , las longitudes de los lados del triángulo son:
, las longitudes de los lados del triángulo son:
![DE =\sqrt{[3-(-2)]^(2)+(2-1)^(2)}](https://img.qammunity.org/2021/formulas/spanish/high-school/7idajg17rahahs4kaiv663ndmyskhnjlko.png)
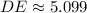
![EF = \sqrt{(5-3)^(2)+[(-5)-2]^(2)}](https://img.qammunity.org/2021/formulas/spanish/high-school/1u1pk1xsl2nynzdbd3qdvg89q276m3op6b.png)
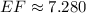
![FD =\sqrt{[(-2)-5]^(2)+[1-(-5)]^(2)}](https://img.qammunity.org/2021/formulas/spanish/high-school/swl1jz91is7n1nn4890b2ym1txh8uonpvc.png)
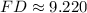
Finalmente, el perímetro requerido para cercar el terreno es:
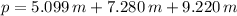
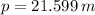
Se requiere 21.599 metros de malla para cercar el terreno.
D) De la Geometría tenemos que el área del triángulo puede calcularse con la siguiente fórmula:
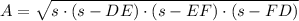 (Eq. 2)
(Eq. 2)
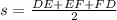 (Eq. 3)
(Eq. 3)
Donde:
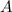 - Área del triángulo, medio en metros cuadrados.
- Área del triángulo, medio en metros cuadrados.
 - Semiperímetro del triángulo, medido en metros.
- Semiperímetro del triángulo, medido en metros.
Si tenemos que
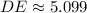 ,
,
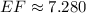 y
y
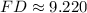 , entonces:
, entonces:
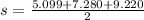
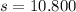
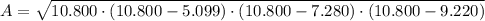
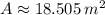
El jardín de Gregorio tiene un área de 18.505 metros cuadrados.