Question

Using the given zero, find one other zero of f(x). 4 - 5i is a zero of f(x).= x4 - 8x3 + 42x2 - 8x + 41.

Answer Choices:

-4 - 5i
1
1 - i
4 + 5i

Answer 1

Since 4 - 5i is a zero of f(x), its conjugate 4 + 5i will also be a zero of f(x). Therefore, the correct answer is 4 + 5i

How to find another zero of the function

To find another zero of the function f(x) given that 4 - 5i is a zero, use the complex conjugate theorem.

Given function:

`f(x).= x^4 - 8x^3 + 42x^2 - 8x + 41.`

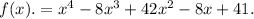
According to the theorem, if a polynomial has complex coefficients and one complex zero is a + bi, then its conjugate, a - bi, is also a zero of the polynomial.

Since 4 - 5i is a zero of f(x), its conjugate 4 + 5i will also be a zero of f(x). Therefore, the correct answer is:

4 + 5i

Answer 2

1 Using the given zero, find one other zero of f(x). 4 - 5i is a zero of f(x).= x4 - 8x3 + 42x2 - 8x + 41. -4 - 5i 1 1 - i 4 + 5i #2 Find a cubic function

Explanation: