Question

The revenue for a company producing widgets is given by y = -20x2 - 50x + 200, where x is the price in dollars for each widget. The cost for the production is given by y = 30x - 10. Determine the price that will allow the production of widget to break even.

Answer 1

1.81 per widget

Explanation:

If you put in the equations in Desmos, you can see where is breaks even

Answer 2

The price is x = $2.779

Explanation:

From the question we are told that

The revenue is
`y = - 20x^2 - 50 x + 200`

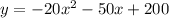
The cost of production is
`y = 30 x - 10`

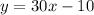
Generally at break even point the cost of production is equal to the revenue

So

`-20x^2 -50x + 200 = 30x-10`

=>
`20x^2 +20 -210 = 0`

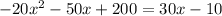
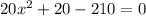
Using the quadratic formula to solve this equation we have that

x = $2.779