Answer:
30
Step-by-step explanation:
Given that
Logan shelves 5 books and
Nathan shelves 6 books
They end shelving the same number of books.
To find:
Smallest number of books each could have shelved?
Solution:
First of all, let us have a look at the definition of Least Common Multiple(LCM) of two numbers.
Least Common Multiple (LCM) of two numbers is the minimum number which is divisible by both the numbers.
Now, looking at the statement of the given question.
We have to find the LCM of both the numbers actually.
Making factors of the numbers:
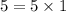

Nothing is common here, therefore the LCM is
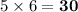 .
.
Smallest number of books shelved = 30