Question

Consider a communication source that transmits packets containing digitized speech. After each transmission, the receiver sends a message indicating whether the transmission was successful or unsuccessful. If a transmission is unsuccessful, the packet is resent. Suppose a voice packet can be transmitted a maximum of 8 times. Assuming that the results of successive transmissions are independent of one another and that the probability of any particular transmission being successful is p, determine the probability mass function of the number of times a packet is transmitted.

Answer 1

The probability mass function is

`F(x) =  [ \left \ 8 } \atop {x}} \right. ] * p^x  *  q^(n - x )`

Explanation:

From the question we are told that

The maximum transmission time is
`n  =  8`

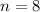
Generally the number of times a packet is transmitted follows a binomial distribution given that the the results of successive transmissions are independent of one another and that the probability of any particular transmission being successful is p

Generally the probability mass function is mathematically represented as

`F(x) =  [ \left \ 8 } \atop {x}} \right. ] * p^x  *  q^(n - x )`

Here x can take values x = 0 , 1 , 2 , 3 , ... , 7