Question

What is the minimum value of F(x)= 10x^{2} -6x-3
3/10 or -39/10

Answer 1

Answer: 3/10

Explanation:

Take the derivative of
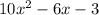`10x^2-6x-3` to get
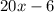`20x-6`. Set that equal to 0 to find the critical points of the function. The critical points is when the slope is either 0 or undefined.

Now do:

`20x-6=0\\20x=6\\x=(6)/(20) = (3)/(10)`

There are quite a few more steps to actually find the minimum, but for this example you can automatically assume its a minimum because it is the only critical point of the function. Ill show you these extra steps tho.

Plug in two numbers into the derivative. One that is less than 3/10 and one that is greater than 3/10. The numbers 0 and 1 are fine. When x = 0, the function is -6. When x = 1, the function is +14. A switch from negative to positive indicates a minimum value