Problem 9
a = 500 = initial amount
b = 1+r/n = 1 + 0.034/52 = 1.000654 = approximate growth factor
The equation goes from
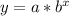 to
to
 where x is the number of weeks and y is the account balance in dollars.
where x is the number of weeks and y is the account balance in dollars.
Plug in y = 700 and isolate x by using logarithms.

It takes about 515 weeks for the account balance to reach $700
This is equivalent to roughly 515/52 = 9.904 years
Answer: 515 weeks
===========================================================
Problem 10
The formula to calculate the monthly payment is not a simple exponential growth or decay function. I'm not sure how your teacher wanted you to answer this question. You'll have to get clarification on it.
If your teacher is asking something along the lines of "$240,000 is invested at a rate of 1.2% compounded bimonthly. How many years does it take to have the investment reach $300,000?" then you could follow these steps below.
a = 240,000 = initial amount
b = 1 + r/n = 1 + 0.012/24 = 1.0005 = growth factor
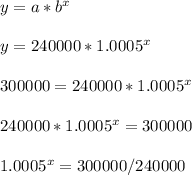
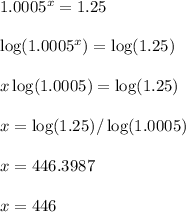
The x represents the number of bimonthly periods. There are 24 bimonthly periods in a year, which means it takes roughly 446/24 = 18.58 years for the starting balance of $240,000 to reach $300,000.
Keep in mind that the steps above are based on the assumption I made at the top of the problem. If that assumption is incorrect, then ignore the steps and answer entirely.