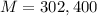Complete Question
1. (12 points) The tennis team at Taft High School has 8 players, and the tennis team at McKinley High School has 7 players. Rebecca is on the team at Taft, and her sister Leah is on the team at McKinley. The two teams are going to play a tournament with 4 rounds. In each round, one player from Taft will play a match against one player from McKinley. Each player can play in at most one match. A schedule for the tournament consists of an ordered list of the names of the players from each school who will play in each of the four rounds. The schedule does not include the results of each match.
(a) How many schedules are there?
(b) How many schedules include neither sister?
Answer:
a

b
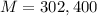
Explanation:
From the question we are told that
The number of players in Taft High School is t = 8
The number of players in McKinley High School is k = 7
The number of rounds is n = 4
The highest number of match each player can play is w = 1
Generally the total number of schedules is
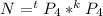
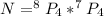
=>
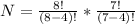
=>
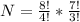
=>
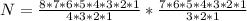
=>

Generally the number of schedules that include neither of the sisters is mathematically represented as
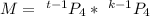
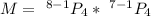
=>
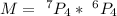
=>
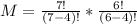
=>

=>
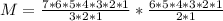
=>