Answer:
6 miles/hr
Explanation:
Given:
Top speed of Brand A scooter goes 2 miles per hour faster than Brand B.
Distance traveled by brand A scooter on its top speed in 3 hours = 24 miles
To find:
The rate at which brand B traveled the same distance at its top speed ?
Solution:
Let the top speed/rate of brand B scooter =
 miles/hr
miles/hr
According to question:
Top speed/rate of brand A scooter =
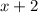 miles/hr
miles/hr
Formula:
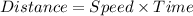
Distance is given to be equal to 24 miles:
24 = (
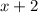 )
)
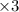 ...... (1)
...... (1)
Solving the above equation by first dividing the equation on both sides with 3:
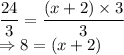
Now subtracting 2 from both the sides:
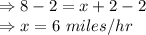
Therefore, the answer is:
Top speed of scooter B is 6 miles/hr.
The if-then moves used to solve the equation (1) are:
Dividing by a non zero number on both sides, then subtracting a number on both sides.