Question

Logarithms:

A law was established, in which it considers that a driver who has more than 0.8 grams of alcohol per liter of blood, is in a state of drunkenness. It is estimated that the risk that a person has of suffering an accident when driving a vehicle under the influence of alcohol is given by the expression
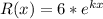
`R(x) = 6 * e^(kx)` , where R(x) is the risk expressed as probability, X is the concentration of alcohol in the blood and K a constant:


A) Calculate the value of the constant K knowing that the concentration of 0.04 g / L of alcohol in the blood (x = 0.04) corresponds to an accident risk of 10% (R = 10)


B) A person who, according to the Law, drives while intoxicated, that is to say 0.8 g / L in blood, what are the risks of suffering an accident?


C) If a driver is under the influence of alcohol, that is 0.3 g / L, what is the risk of having an accident?

(Develop each one step by step)

Answer 1

• A) k = 18.75
• B) R(0.8) = 161419
• C) R(0.3) = 275

Explanation:

Given expression

• R(x) = 6*e^(kx)

A) Given

• x = 0.04
• R = 10

Solving for k

• 10 = 6*e^(0.04k)
• e^(0.04k) = 10/6
• ln (e^0.04k) = ln (1.6666)
• 0.04k = 0.51
• k = 0.51/0.04
• k = 12.75

B) Given

• x = 0.8
• R= ?

The value of R(0.8) is:

• R(0.8) =
• 6*e^(0.8*12.75) =
• 6*e^(10.2) =

• 161419 rounded

C) Given

• x = 0.3
• R = ?

The value of R(0.3) is:

• R(0.3) =
• 6*e^(0.3*12.75) =
• 6*e^(3.825) =

• 275 rounded