Answer:
(a) 99.865%
(b) 0.135%
Step-by-step explanation:
Given that the weight of the boxes are normally distributed.
The average weight of the particular box,
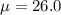 ounce
ounce
The standard deviation of weight,
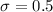 ounce.
ounce.
Let
 be the standard normal variable,
be the standard normal variable,

And, the probability of the boxes having weight x ounces is
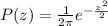
For
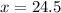 ,
,

(a) For the boxes having weight more than 24.5 ounces:
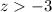
So, the probability of boxes for
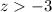 is
is
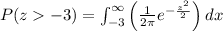
=0.99865
So, the percent of the boxes weigh more than 24.5 ounces is 99.865%.
(b) For the boxes having weight less than 24.5 ounces: z<-3
So, the probability of boxes for z<-3 is
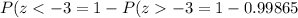
=0.00135
So, the percent of the boxes weigh more than 24.5 ounces is 0.135%.