Answer:
The recursive rule is
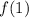 = first term;
= first term;
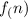 =
=
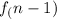 + d
+ d
f(1) = 55;
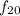 =
=
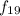 + 10
+ 10
The explicit rule is f(n) = f(1) + (n - 1)d
f(20) = 245
Explanation:
The recursive rule of the arithmetic sequence is
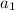 = first term;
= first term;
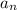 =
=
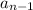 + d
+ d
Where:
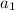 is the first term in the sequence
is the first term in the sequence
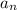 is the nth term in the sequence
is the nth term in the sequence
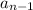 is the term before the nth term
is the term before the nth term
- d is the common difference.
The explicit rule of the arithmetic sequence is
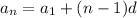
where:
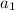 is the first term in the sequence
is the first term in the sequence
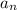 is the nth term in the sequence
is the nth term in the sequence
- d is the common difference
∵ The first 4 terms of the sequence are 55, 65, 75, 85
∴
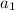 = 55
= 55
∵ d = 65 - 55
∴ d = 10
∵ We need to find the 20th term
∴ n = 20
∵ The recursive rule is
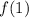 = first term;
= first term;
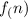 =
=
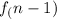 + d
+ d
→ Substitute the values of
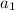 , n, and d in recursive rule
, n, and d in recursive rule
∴ f(1) = 55;
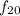 =
=
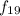 + 10
+ 10
∵ The explicit rule is f(n) = f(1) + (n - 1)d
→ Substitute the values of n and d to find it
∴ f(20) = 55 + 19(10) = 245
∴ f(20) = 245