Question

Learning Task 3. Solve for the variable of the following quadratic equations

A. by extracting square roots.
1. x2 = 169
4. (x - 2)2 = 16
2. 9b2 = 25
5. 2(t - 3)2 - 72 = 0
3. (3y - 1)2 = 0
B. by factoring
1. x2 + 7x = 0
3. x2 + 5x - 14 = 0
2. m2 + 8m = -16
4. 2y2 +8y - 10= 0
C. by completing the square.
1. x2 + 5x + 6= 0
2. x2 + 2x = 8
3. 2x2 + 2x = 24
D. using quadratic formula.
1. x2 + 5x = 14
2. 2x2 +8x - 10= 0
3. 2x2 + 3x = 27​

Answer 1

A. By extracting square roots

1. x = 13

4. x = 6

2. b = 5/3

5. t = 9

3. y = 1/3

B. By factoring

1. x = -7

3. x = -7 or x = 2

2. m = -8 or m = -2

4. y = -5 or y = 1

C. By completing the square

1. x = 2 or x = 3

2. x = 10 or x = -8

3. x = 3 or x = -4

D. Using the quadratic formula

1. x = 2 or x = -7

2. x = 1 or x = -5

3. x = 3 or x = -4.5.

Explanation:

A. By extracting square roots

1. x² = 169

Extracting square roots from both sides of the equation gives;

√(x²) = x and √169 = 13

∴ √(x²) = √169 = 13

x = 13

4. (x - 2)² = 16

Extracting square roots from both sides of the equation gives;

√(x - 2)²= √16 = 4

However;

√(x - 2)² = x - 2

∴ x - 2 = √16 = 4

x - 2 = 4

x = 4 + 2 = 6

x = 6

2. 9·b² = 25

√(9·b²) = √25 = 5

√(9·b²) = √9 × √(b²) = 3·b

∴ 3·b = √25 = 5

3·b = 5

b = 5/3

5. 2·(t - 3)² - 72 = 0

2·(t - 3)² = 72

(t - 3)² = 72/2 = 36

t - 3 = √36 = 6

t = 6 + 3 = 9

t = 9

3. (3·y - 1)² = 0

√(3·y - 1)² = √0

∴ 3·y - 1 = 0

3·y = 0 + 1 = 1

y = 1/3

B. By factoring

1. x² + 7·x = 0

By factoring, we have;

x·(x + 7) = 0

(x + 7) = 0/x = 0

x + 7 = 0

x = 0 - 7 = -7

x = -7

3. x² + 5·x - 14 = 0

Noting that 7 × (-2) = -14 and 7 + (-2) = 5, we get;

x² + 5·x - 14 = (x + 7)·(x - 2) = 0

∴ x = -7 or x = 2

2. m² + 8·m = -16

m² + 8·m + 16 = 0

Which gives;

m² + 8·m + 16 = (m + 8) × (m + 2) = 0

m = -8 or m = -2

4. 2·y² + 8·y - 10 = 0

Which gives;

2·(y² + 4·y - 5) = 0

y² + 4·y - 5 = 0/2 = 0

y² + 4·y - 5 = (y + 5) × (y - 1) = 0

y = -5 or y = 1

C. By completing the square

1. x² + 5·x + 6 = 0

x² + 5·x = -6

Adding (5/2)² to both sides of the equation gives;

x² + 5·x + (5/2)² = -6 + (5/2)²

Which gives;

(x + 5/2)² = -6 + (5/2)² = 1/4

x + 5/2 = ±√(-6 + (5/2)²) = ±√(1/4)

x + 5/2 = ±1/2

x = 5/2 - 1/2 or x = 5/2 + 1/2

∴ x = 2 or x = 3

2. x² + 2·x = 8

x² + 2·x + (2/2)² = 8 + (2/2)²

2/2 = 1 and (2/2)² = 1² = 1

∴ x² + 2·x + (2/2)² = 8 + (2/2)² gives;

x² + 2·x + 1 = 8 + 1 = 9

(x + 1)² = 9

x + 1 = ±√9

x = 1 + 9 or x = 1 - 9

x = 10 or x = -8

3. 2·x² + 2·x = 24

2·(x² + x) = 24

x² + x = 24/2 = 12

x² + x = 12

x² + x + (1/2)² = 12 + (1/2)²

(x + 1/2)² = 12 + (1/2)² = 49/4

√(x + 1/2)² = √(49/4) = ±7/2 = ± 3.5

x + 1/2 = ±3.5

x = -1/2 + 3.5 or x = -1/2 - 7/2

x = -0.5 + 3.5 or x = -0.5 - 3.5

x = 3 or x = -4

D. Using the quadratic formula

1. x² + 5·x = 14

Simplifying, gives;

x² + 5·x - 14 = 0

The quadratic formula for the equation, a·x² + b·x + c = 0, is given as follows;

`x = \frac{-b\pm \sqrt{b^(2)-4\cdot a\cdot c}}{2\cdot a}`

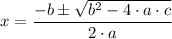
Comparing with the equation in the question, we get;

`x = \frac{-5\pm \sqrt{5^(2)-4* 1*(-14)}}{2* 1} = (-5\pm √(81))/(2) = (-5\pm 9)/(2) = (-5+ 9)/(2) \ or (-5 - 9)/(2)`

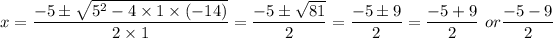
x = 4/2 or x = -14/2

x = 2 or x = -7

2. 2·x² + 8·x - 10 = 0

quest

2. 2·x² + 8·x - 10 = 0

`x = \frac{-8\pm \sqrt{8^(2)-4* 2*(-10)}}{2* 2} = (-8\pm √(144))/(4) =(-8+ 12)/(4) \ or (-8 - 12)/(4)`

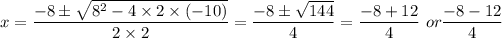
x = 4/4 or x = -20/4

x = 1 or x = -5

3. 2·x² + 3·x = 27

Rewriting the above equation in the form a·x² + b·x + c = 0, we get;

2·x² + 3·x - 27 = 0

Which gives;

`x = \frac{-3\pm \sqrt{3^(2)-4* 2*(-27)}}{2* 2} = (-3\pm √(225))/(4) =(-3+ 15)/(4) \ or (-3 - 15)/(4)`

x = 12/4 = 3 or x = -18/4 = -4.5

x = 3 or x = -4.5.