Question

The function f(x) = (x - 4)(x - 2) is shown below. What is true about the domain and range of the function?​

Answer 1

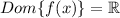`Dom\{f(x)\} = \mathbb{R}` (Since polinomial functions are continuous)

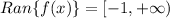`Ran\{f(x)\} = [-1, +\infty)` (As this quadratic function has an absolute minimum, represented by its vertex)

Explanation:

Graphically speaking, quadratic functions are represented by parabolas. In this case, we have a parabola in factorized form. From Theory of Functions, we get that domains of function represents the set of values of
`x` so that exist an image, whose set is known as range is represented by values of
`f(x)`.

`x` is represented by horizontal axis in the figure, whereas
`f(x)` is represented by the vertical axis. By using this approach we get that domain and range of the function are, respectively:

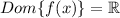`Dom\{f(x)\} = \mathbb{R}` (Since polinomial functions are continuous)

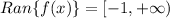`Ran\{f(x)\} = [-1, +\infty)` (As this quadratic function has an absolute minimum, represented by its vertex)