Question

Please help i will give you 100 points

Answer 1

x = 50.5°

Explanation:

In order to solve, get to know about the sine rule:

`\bf Sine \ Rule = (A)/(sinA) = (B)/(sinB)= (C)/(sinC)`

Solve for BD:

`\sf (BD)/(sin(50)) = (5.6)/(sin(78))`

`\sf BD = (5.6(sin(50)))/(sin(78))`

`\sf BD = 4.385686657 \ cm`

Then find angle D = 180° - 78° = 102°

Solve for angle C

`\sf (4.385686657)/(sinC) = (9.3)/(sin(102))`

`\sf C = sin^(-1)((4.385686657sin(102))/(9.3) )`

`\sf C = 27.37 ^(\circ \:)`

Total Sum of interior angles of a triangle is 180°

`\sf B + C + D = 180^\circ`

`\sf x + 27.37^\circ + 102^\circ = 180^\circ`

`\sf x = 180^\circ - 102^\circ - 27.37^\circ`

`\sf x = 50.53^\circ`

`\sf x = 50.5^\circ \ \ \ (rounded \ to \ nearest \ 3 \ significant \ figure)`

Answer 2

x = 50.5° (3 sf)

Explanation:

Sine Rule for side lengths

`\sf (a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

(where A, B and C are the angles and a, b and c are the sides opposite the angles)

Find BD:

`\implies \sf (BD)/(\sin BAD)=(AB)/(\sin BDA)`

`\implies \sf (BD)/(\sin 50^(\circ))=(5.6)/(\sin 78^(\circ))`

`\implies \sf BD=(5.6\:sin 50^(\circ))/(\sin 78^(\circ))`

`\implies \sf BD=4.385686657...cm`

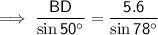
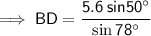
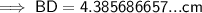
Angles on a straight line sum to 180°

⇒ ∠ADB + ∠BDC = 180°

⇒ 78° + ∠BDC = 180°

⇒ ∠BDC = 102°

Sine Rule for angles

`\sf (\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

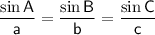
(where A, B and C are the angles and a, b and c are the sides opposite the angles)

Find ∠BCD:

`\implies \sf (\sin BCD)/(BD)=(\sin BDC)/(BC)`

`\implies \sf (\sin BCD)/(4.385...)=(\sin 102^(\circ))/(9.3)`

`\implies \sf BCD=\sin^(-1)\left((4.385...\sin 102^(\circ))/(9.3)\right)`

`\implies \sf BCD=27.46935172...^(\circ)`

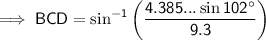
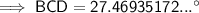
The interior angles of a triangle sum to 180°

⇒ ∠CBD + ∠BDC + ∠BCD = 180°

⇒ x + 102° + 27.469...° = 180°

⇒ x = 50.53064828...°

⇒ x = 50.5° (3 sf)