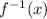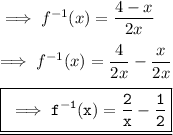Answer:

Explanation:
A function is given to us and we need to find its inverse . So the given function is ,
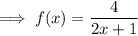
1) So ,let us take f(x) = y . Equation becomes ,
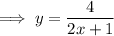
2) Firstly replace x with y and y with x. We get ,
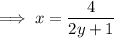
3) Now , solve for y.
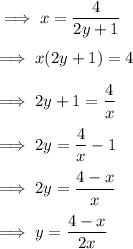
4) Now replace y with