Question

Ann will rent a car for the weekend. She can choose one of two plans. The first plan has an initial fee of $43.98 and costs an additional $0.14 per mile driven. The second plan has an initial fee of $57.98 and costs an additional $0.12 per mile driven. How many miles would Ann need to drive for the two plans to cost the same?

Answer 1

700 miles

Explanation:

Let's write the expressions for each plan.

Plan 1 has an initial fee of $43.98 and an additional $0.14 per mile m.

So, we can write the following expression:

`43.98+0.14m`

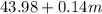
Plan 2 has an initial fee of $57.98 and an additional cost of $0.12 per mile.

So, we can write the following expression:

`57.98+0.12m`

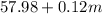
We want to find after how many miles Ann needs to drive for the two plans to cost the same. So, let's set the two expressions equal to each other and solve for m:

`43.98+0.14m=57.98+0.12m`

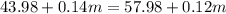
Subtract 43.98 from both sides:

`0.14m=14+0.12m`

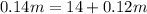
Subtract 0.12m from both sides:

`0.02m=14`

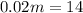
Divide both sides by 0.02:

`m=700`

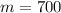
So, after 700 miles, the price of the two plans will cost the same.

Further notes:

This means that if Ann is driving for less than 700 miles, Plan 1 is the cheaper choice since it costs the least to begin with.

However, if Ann is going to drive for more than 700 miles, Plan 2 is the cheaper choice since it has a lower cost per mile additional cost.