Answer:
B
Explanation:
We have the equation:
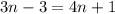
Let's solve for n. To do so, we want to isolate it.
Let's use the subtraction property of equality to subtract 3n from both sides:
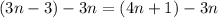
The left side will cancel...
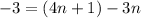
Subtract on the right:

Remember that 1n is the same as just n. So:
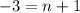
Now, let's use the subtraction property of equality again to subtract 1 from both sides:
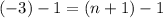
The right side will cancel. Subtract on the left:
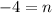
Symmetric property:

So, our answer is B.
And we're done!