Answer:
1)
Nicole:
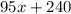
Milan:
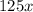
2)

Explanation:
Question 1)
We know that Nicole opened her account with a starting amount of $240. She also puts in $95 per month.
So, we can write the following expression:
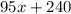
Where 240 represents the initial deposit of $240 and the 95x represents the $95 for x months.
Milan opened his account with no starting amount, and he's putting in $125 per month.
So, we can write the following expression:
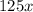
Since he didn't put anything at the start, out initial deposit is simply 0. The 125x represents the $125 for x months.
Question 2)
We want to write an equation that shows when the two accounts will have an equivalent balance.
So, we can simply set the two expressions above equal to each other:

And we're done!
Notes:
Let's solve for x to determine when the two accounts will have the same amount of money. Subtract 95x from both sides:

Divide both sides by 30:
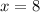
So, after 8 months, the amount in Nicole's and Milan's account will be equivalent.