Question

Find an equation of the circle and sketch it if it has: Center on y=4, tangent x-axis at (–2, 0)

Answer 1

`(x+2)^2+(y-4)^2=16`

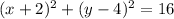
OK, lets start by drawing a basic graph (the first one) so we can visualize.

We already know that the y coordinate of the circle's center is
`4`.

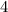We know that the circle is tangent to the
`X` axis at
`(-2,0)`

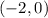
That means the x coordinate of the center has to be
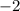`-2`, as the tangent is a point on the edge of the circle that touches a line at exactly one point.

The radius is the distance from the center of the circle to its edge. We know the center's location now, it is
`(-2, 4)` and a point on the edge of the circle (the tangent point) which is
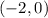`(-2,0)`. so the distance between the points is 4 which is the radius (you can use the distance formula, but it's quite oblivious.)

We can imagine the circle should look like this (the second one):

Now we can piece together an equation

The equation of a circle is
`(x-h)^2+(y-k)^2=r^2` where
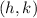`(h,k)` is the center and
`r` is the radius. When we put the numbers in: we get
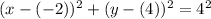`(x-(-2))^2+(y-(4))^2=4^2` which can be simplified into
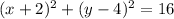`(x+2)^2+(y-4)^2=16` which is the answer.

Explanation: