Question

Which equation relates y to the x for the values in the table?

a) y= 1/2 times (5/2) x

b) y= 2 times (3/4) x

c) y= 3/4x plus 2

d) y= 7/2x minus 3/4

Answer 1

D

Explanation:

First, we can determine what type of relationship we are dealing with by examining the table.

From x = 1 to x = 2, the y-value increased by 14/4 (25/4-11/4).

From x = 2 to x = 3, the y-value also increased by 14/4 (39/4-25/4)

And from x = 3 to x = 4, the y-value still increased by 14/4 (53/4-39/4).

Therefore, we can conclude that our table represents a linear relationship.

And since it increases by 14/4 or 7/2 for every x, this means that our slope is 7/2.

The only choice that represents a linear equation with a slope of 7/2 is D. So, the correct answer is D.

However, we can confirm our answer by writing our equation. We can use the point-slope form:

`y-y_1=m(x-x_1)`

Where m is the slope and (x₁, y₁) is a point.

Let's substitute 7/2 for m. We can pick any point, so I'm going to use (1, 11/4) for (x₁, y₁).

Substitute:

`\displaystyle y-(11)/(4)=(7)/(2)(x-1)`

Distribute:

`\displaystyle y-(11)/(4)=(7)/(2)x-(7)/(2)`

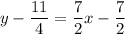
Add 11/4 to both sides. Note that 7/2 is the same as 14/4. So:

`\displaystyle y=(7)/(2)x-(14)/(4)+(11)/(4)`

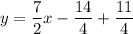
Add:

`\displaystyle y=(7)/(2)x-(3)/(4)`

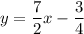
So, our answer is D.

And we're done!