Question

Simplify x = cos[2 arcsin(3/5)].

-7/25
7/25
4/5

Answer 1

7/25

Explanation:

Let
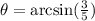`\theta= \arcsin((3)/(5))` so we have
`x=\cos(2\theta)`

As
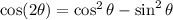`\cos(2\theta)=\cos^2\theta-\sin^2\theta`, we'll have
`\cos[2\arcsin((3)/(5))]=\bigr[\cos(\arcsin((3)/(5)))\bigr]^2-\bigr[(\sin(\arcsin((3)/(5)))\bigr]^2`

To determine
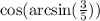`\cos(\arcsin((3)/(5)))`, construct a right triangle with an opposite side of 3 and a hypotenuse of 5. This is because since
`\theta=\arcsin((3)/(5))`, then
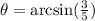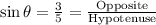`\sin\theta=(3)/(5)=\frac{\text{Opposite}}{\text{Hypotenuse}}`. If you recognize the Pythagorean Triple 3-4-5, you can figure out that the adjacent side is 4, and thus,
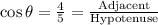`\cos\theta=(4)/(5)=\frac{\text{Adjacent}}{\text{Hypotenuse}}`. This means that
`\cos(\arcsin((3)/(5)))=(4)/(5)`.

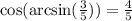Hence,
`\cos[2\arcsin((3)/(5))]=((4)/(5))^2-((3)/(5))^2=(16)/(25)-(9)/(25)=(7)/(25)`