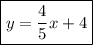Question

What is the equation of the line​

Answer 1

`\boxed {y = (4)/(5)x + 4}`

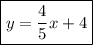
Explanation:

Determine the graph by using the rise over run. Since the line shows that it is increasing (up), then the slope is positive:

Rise =
`4`

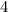
Run =
`6`

`m = (4)/(5)`

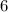
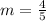
After you have found the slope, find the y-intercept, which when the line crosses the y-axis:

Y-intercept =
`4`

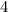
-Since you now have the slope and y-intercept, use them to form a Slope-Intercept form:

`y = mx + b`

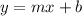
Apply them to the equation:

`\boxed {y = (4)/(5)x + 4}`