Question

The vertices of a right triangle are (0, 0), (1, 0), and (0, 1).

If the triangle is dilated by a factor of 3 with respect to the origin, which coordinate pair cannot be one of the vertices?


Question options:


(3, 3)



0, 0)



(0, 3)



(3, 0)

Answer 1

(3,3)

Explanation:

Given

`Vertices: (0,0)\ (1,0)\ (0,1)`

`Scale\ Factor = 3`

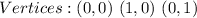
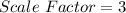
Required

Determine which can't be any of the new vertices

First, we need to determine the new vertices:

`New\ Vertex = Scale\ Factor * Old\ Vertex`

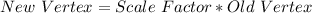
For (0,0):

`New\ Vertex = 3 * (0,0)`

`New\ Vertex = (3 * 0,3 * 0)`

`New\ Vertex = (0,0)`

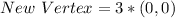
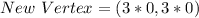
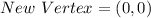
For (1,0):

`New\ Vertex = 3 * (1,0)`

`New\ Vertex = (3 * 1,3 * 0)`

`New\ Vertex = (3,0)`

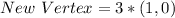
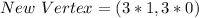
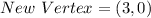
For (0,1):

`New\ Vertex = 3 * (0,1)`

`New\ Vertex = (3 * 0,3 * 1)`

`New\ Vertex = (0,3)`

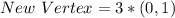
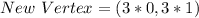
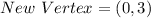
Comparing the calculated new vertices to the list of given options; (3,3) can't be any of the new vertices of the new triangle