Answer:
a) 4 roots
b) x = 1 and x = -3

d) see attached
Explanation:
Given function:
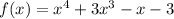
Part (a)
From inspection of the function, the highest exponent of the polynomial is 4. Therefore, it is expected that the polynomial will have 4 roots.
Part (b)
To find the rational roots, find values of x where
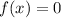
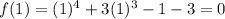
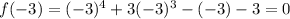
Therefore, the rational roots are: x = 1 and x = -3
Part (c)
As there are only 2 rational roots, the other 2 roots must be complex roots. To find these, first factor the polynomial using the 2 rational roots found in part (b):
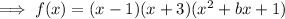
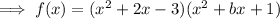
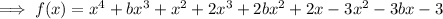
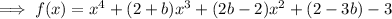
Compare coefficients to find b:
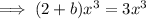

Therefore the fully factored function is:

Therefore:
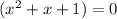
To find the complex roots, use the quadratic formula
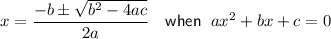
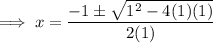
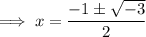
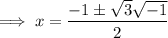
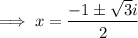
Therefore, all the roots of the function are:
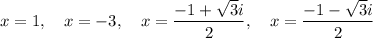
Part (d)
End behaviors:
As the degree of the function is even and the leading coefficient is positive, the end behaviors are:

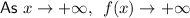
y-intercept
Substitute x = 0 into the function:
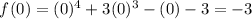
Therefore, the y-intercept is (0, -3)
To find the approximate x-coordinates of the turning points (stationary points), differentiate the function, set it to zero, then solve for x:

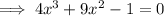
Using a calculator, x ≈ -2.2, x ≈ -0.4, x ≈ 0.3
Therefore the approximate coordinates of the turning points are:
(-2.2, -9.3), (-0.4, -2.7) and (0.3, -3.2)
We don't need to plot these points, they merely help us with the approximate shape of the curve.