Question

The length of a rectangle is 7 more than the width. The area is 744 sqaure yards, find the length and width of the rectangle​

Answer 1

• Length of rectangle is 31 yards and Width is 24 yards.

Given:

• The length of a rectangle is 7 more than the width.
• The area is 744 sqaure yards

Solution:

Let's assume Width of rectangle be x and Length of rectangle be x + 7 respectively.

Using formula

`\\ \: \: \: \: \pink{ \dashrightarrow \: \: \: \: \sf { \underbrace{Area_((Rectangle)) = Length × Width }}} \\ \\`

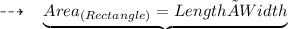
On Substituting the required values, we get;

`\\ \: \: \: \: \dashrightarrow \: \: \: \: \sf (x)(x + 7) = 744 \\ \\ \\ \: \: \: \: \dashrightarrow \: \: \: \: \sf {x}^(2) + 7x = 744 \\ \\ \\ \: \: \: \: \dashrightarrow \: \: \: \: \sf {x}^(2) + 7x - 744 = 0 \\ \\ \\ \: \: \: \: \dashrightarrow \: \: \: \: \sf {x}^(2) + 31x - 24x - 744 = 0 \\ \\ \\ \: \: \: \: \dashrightarrow \: \: \: \: \sf x(x + 31) - 24 (x + 31) = 0 \\ \\ \\ \: \: \: \: \dashrightarrow \: \: \: \: \sf (x + 31)(x - 24) = 0 \\ \\ \\ \: \: \: \: \dashrightarrow \: \: \: \: \sf x = 24 \: or \: - 31 \\ \\`

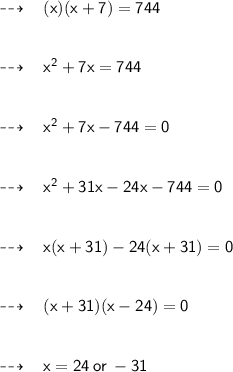
As we know that width of the rectangle can't be negative. So x = 24

Hence,

• Width of rectangle = x = 24 yards
• Length of the rectangle = x + 7 = 31 yards

`\therefore`Length of rectangle is 31 yards and Width is 24 yards.