Answer:
Explanation:
Dimensions of the rectangular park = 4 inches by 6 inches
Since scale factor =
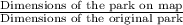 =
=
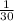

Length of the original park = 120 miles
Similarly, width of the park = 180 miles
Area of the park = Length × Width
= 120 × 180
= 21600 square miles
Therefore, area of the original park is 21600 square miles.
Formula for the ratio of area of the park on map and original park is,
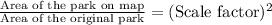

Scale factor =
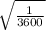
=
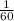
Scale factor to reproduce the map so that it fits in the brochure will be 1 inch for every 60 miles.