Question

A long jumper lifts off 3 m after starting his run, and lands 6 m later. When he is 8 m from the start line, he is 5 cm above and he ground. Write the equation of a parabola that models his path through the air, where x is horizontal distance from the start line in m and y is his height, in cm.

Answer 1

The equation of the parabola that models the path of the long jumper through the air is
`y = -x^(2)+12\cdot x -27`.

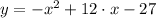Explanation:

Mathematically, we know that parabolas are second-order polynomials and every second-order polynomials, also known as quadratic functions, can be constructed by knowing three different points of the curve. The standard form of the parabola is:

`y = a\cdot x^(2)+b\cdot x + c`

Where:

`x` - Horizontal distance from the start line, measured in meters.

`y` - Height of the long jumper, measured in meters.

`a`,
`b`,
`c` - Polynomial constants, measured in
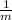`(1)/(m)`, dimensionless and meters, respectively.

If we know that
`(x_(1),y_(1)) = (3\,m, 0\,m)`,
`(x_(2),y_(2)) = (8\,m, 0.05\,m)` and
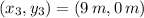`(x_(3), y_(3)) = (9\,m, 0\,m)`, this system of linear equations is presented below:

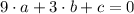`9\cdot a + 3\cdot b + c = 0` (Eq. 1)

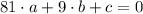`81\cdot a + 9\cdot b + c = 0` (Eq. 2)

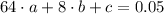`64\cdot a + 8\cdot b + c = 0.05` (Eq. 3)

The coefficients of the polynomial are, respectively:

`a = -(1)/(100)`,
`b = (3)/(25)`,
`c = -(27)/(100)`

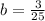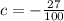
The equation of the parabola that models the path of the long jumper through the air is
`y' = -(1)/(100)\cdot x^(2)+(3)/(25)\cdot x -(27)/(100)`.

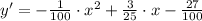But we need
`y` measured in centimeters, then, we use the following conversion:

`y = 100\cdot y'`

Then, we get that:

`y = -x^(2)+12\cdot x -27`

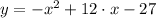
Where
`x` and
`y` are measured in meters and centimeters, respectively.

The equation of the parabola that models the path of the long jumper through the air is
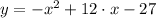`y = -x^(2)+12\cdot x -27`.