Question

A family bought a total of 16 adult and child tickets to a magic show.adult tickets are 10.50 each and child tickets are 7.50 each .the family paid a total of $141

Answer 1

There were 7 adults and 9 children paying tickets to the magic show

Explanation:

System of Equations

A system of equations consists of more than one variable related to more than one equation. The question we're working on requires to know two variables: the number of children and the number of adults that paid to a magic show.

Let's call x to the number of adults and y to the number of children. The first condition states there are a total of 16 persons in the group. This can be written as:

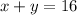`x+y=16` [1]

We also know the adult tickets cost $10.50 each and child tickets cost $7.50 each. This means the total amount paid for the tickets is:

`total\ paid = 10.50*x+7.50*y`

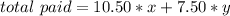
We are given this total, thus

`10.50*x+7.50*y=141` [2]

The system formed by [1] and [2] must be solved to answer the question. Let's solve [1] for x:

`x=16-y`

And substitute x in [2]:

`10.50*(16-y)+7.50*y=141`

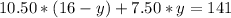
Operating:

`10.50*16-10.50*y+7.50*y=141`

`-10.50*y+7.50*y=141-10.50*16`

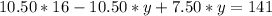
Joining like terms and operating on the right side:

`-3y=-27`

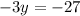
Solving:

`\displaystyle y=(-27)/(-3)`

`\boxed{y=9}`

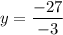
The value of x is calculated by

x=16-y=16-9

`\boxed{x=7}`

This means there were 7 adults and 9 children paying tickets to the magic show