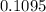Question

A certain form of cancer is known to be found in women over 60 with probability of 0.07. A blood test exists for the detection of the disease, but the test is not infallible. In fact, it is known that 10% of the time the test gives a false negative (i.e. the test incorrectly gives negative result when the woman actually has the cancer) and 5% of the time the test gives false positive (i.e. incorrectly gives a positive result when the woman actually does not have the cancer). What is the probability that a randomly selected woman over 60 will test positive?

Answer 1

Throughout the segment below, the definition including its particular question is mentioned.

Explanation:

The probability of developing cancer

= 0.07

The probability of someone not getting cancer

= 1 - 0.07

= 0.93

Provided that if women have cancer, the risk of someone not testing positive is:

= 0.10

Therefore, if a female requires cancer, the risk of testing positive

= 1 - 0.10

= 0.90

The Probability of positive test

= 0.055 (whenever a woman does not have cancer)

Therefore, whenever a woman does not have cancer, the risk of not testing positive will be:

= 1 - 0.05

= 0.955

Now,

By using the law of conditional probability, we get

⇒
`P((B)/(A) ) = (P(A \ and \ B))/(P(A))`

⇒
`P (A \ and \ B) = P(A)* P(B)`

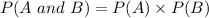
⇒ P (having cancer as well as positive tests) = P(having cancer) × P(Effective results, because she has cancer)

⇒
`0.07* 0.90`

⇒
`0.063`

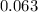
Correspondingly,

P (not getting cancer and testing effective or positive)

=
`0.93* 0.05`

=
`0.04655`

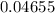
P (with a good test result)

=
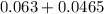
`0.063 + 0.0465`

=
`0.1095`