Question

The USC Trojan football team bus is heading to an away game, traveling on a long, straight road at a constant speed of 28.0 m/s. All of a sudden, at t = 0, a car full of students from the opposing team cuts in front of the bus, at a mere distance of 70.0 m ahead of the bus, moving in the same direction with a constant velocity of 6.00 m/s. The panic brake deceleration of the bus is 3.00 m/s2 . a) (10 Points) If the bus begins braking at t = 0, how much time will elapse until the bus and car collide? b) (5 Points) How far down the road, from the original position of the bus, will the collision occur? c) (10 Points) What would the acceleration of the bus have to be for the collision to be avoided?

Answer 1

a. 17.34 s. b. 104.51 m c. -7.16 m/s²

Step-by-step explanation:

a. The distance, d moved by the car at constant speed v = 6.00 m/s in time t which they collide is d = vt. The distance d' moved by the bus from its initial position 70 m away from the car with a constant velocity u = 28.0 m/s and deceleration a = -3.00 m/s² is d' = 70 + ut + 1/2at².

At collision, s = d

vt = 70 + ut + 1/2at²

substituting the values of the variables, we have

6t = 70 + 28t + 1/2(-3)t²

6t = 70 + 28t - 1.5t²

collecting like terms, we have

1.5t² + 6t - 28t - 70 = 0

1.5t² - 22t - 70 = 0

using the quadratic formula to find t, we have

`t = \frac{-(-22) +/- \sqrt{(-22)^(2) - 4 X -70 X 1.5} }{2 X 1.5} \\t = (22 +/- √(484 + 420) )/(3) \\\\t = (22 +/- √(904) )/(3) \\\\t = (22 +/- 30.01 )/(3) \\\\t = (22 - 30.01 )/(3) or (22 + 30.01 )/(3) \\t = (-8.01 )/(3) or (52.01 )/(3) \\\\t = -2.67 s or 17.34 s`

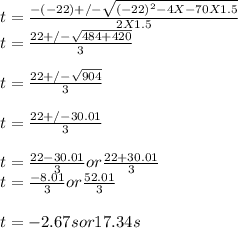
We take the positive value.

So t = 17.34 s.

So, 17.34 s elapses before the bus and car collide.

b. Since the distance covered by the bus is d' = 70 + ut + 1/2at², this is how far down the road the collision occurs.

Substituting the values of the variables, we have

d' = 70 + 28 m/s × 17.34 s + 1/2(-3 m/s²)(17.34)²

d' = 70 + 485.52 - 451.01

d'= 104.51 m

c. To just avoid the collision, the bus must decelerate in the distance of 104.51 m from the car to the speed of the car. So using

v² = u² + 2ad' where v = 6.00 m/s, u = 28.0 m/s and d' = 104.51 m

the acceleration is thus

a = (v² - u²)/d'

a = ((6 m/s)² - (28 m/s)²)/104.51 m

a = (36 m²/s² - 784 m²/s²)/104.51 m

a = -748 m²/s² ÷ 104.51 m

a = -7.16 m/s²