Question

Race: Blythe and Geoff compete in a 1-km race. Blythe’s strategy is to run the first 600 m of the race at a constant speed of 4 mm/ss, and then accelerate with constant acceleration to her maximum speed of 7.5 mm/ss, which takes her 1 min, and finish the race at that speed. Geoff decides to accelerate with constant acceleration to his maximum speed of 8 m/s at the start of the race and to maintain that speed throughout the rest of the race. It takes Geoff 3 min to reach his maximum speed. Who wins the race?

Answer 1

From the value of each person's time to finish the race, it can be concluded that Geoff will win the race.

Step-by-step explanation:

Given;

total distance to be covered, d = 1000 m

first distance covered by Blythe,
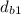`d_b_1` = 600 m

constant speed of Blythe at the first stage,
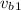`v_b_1` = 4 m/s

final speed of Blythe,
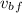`v_b_f` = 7.5 m/s

time of Blythe's constant acceleration,
`t` = 1 min = 60 s

initial speed of Geoff,
`v_g_1` = 0

final speed of Geoff,
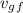`v_g_f` = 8 m/s

time of Blythe's constant acceleration,
`t` = 3 min = 180 s

The acceleration of Blythe is given as;

`a_b = (dv)/(dt) = (7.5 - 4)/(60) = 0.0583 \ m/s^2`

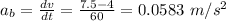
distance covered by Blythe during this acceleration is given as;

`d_(a_b) = v_b_1t + (1)/(2) a_b t^2\\\\d_(a_b) = 4*60 + (1)/(2)(0.0583) (60)^2\\\\d_(a_b) = 344.94 \ m`

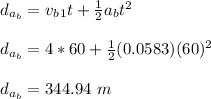
The remaining distance covered by 7.5 m/s is given as;

`d_f = d - (600 + 344.94)\\\\d_f = 1000- (944.94)\\\\d_f = 55.06 \ m`

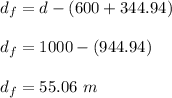
The total time for Blythe to covere the entire distance = time taken to cover 600 m + time taken to cover 344.94 m + time taken to cover 55.06 m

`t_b = (600 \ m)/(4 \ m/s)\ +\ 60 s \ + \ (55.06 \ m)/(7.5 \ m/s) \\\\t_b = 150 s \ + \ 60s \ + \ 7.34 s\\\\t_b = 217.34 s`

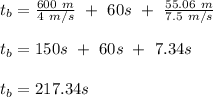
The acceleration of Geoff is given as;

`a_g = (dv)/(dt) = (8 -0)/(180) = 0.044 \ m/s^2`

distance covered by Geoff during this acceleration is given as;

`d_(a_g) = v_g_1 + (1)/(2)a_gt^2\\\\ d_(a_g) =0 + (1)/(2)(0.044)(180)^2\\\\ d_(a_g) = 712.8 \ m`

The remaining distance covered by 8 m/s is given a;

`d_f = 1000 \ m - 712.8 \ m\\\\d_f = 287.2 \ m`

The total time for Geoff to covere the entire distance = time taken to cover 712.8 m + time taken to cover 287.2 m

`t_g = 180s + (287.2 \ m)/(8 \ m/s) \\\\t_g = 180s + 35.9 s\\\\t_g = 215.9 s`

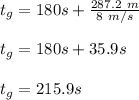
Therefore, from the value of each person's time to finish the race, it can be concluded that Geoff will win the race