Question

A set of children’s blocks contains three shapes: long, flats, and cubes. There are three times as many longs as cubes and 30 fewer flats than longs. if there are 600 blocks in all how many Long’s are there

Answer 1

There are 270 longs

Explanation:

Equations

We must write the problem into a mathematical model that allows us to apply the properties of basic algebra and solve for the variable which must be adequately set up.

We have three unknowns: the number of long blocks, flats blocks, and cubes. The conditions are given:

• There are three times as many longs as cubes
• There are 30 fewer flats than longs.
• There are 600 blocks in all

For the equation to be easier solved, let's set the variable as the number of cubes:

x = number of cubes

Considering the first condition, we have

3x = number of longs

3x-30 = number of flats

And finally:

`x + 3x+3x-30=600`

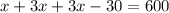
Joining like terms:

`7x=630`

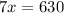
Solving for x

`\displaystyle x=(630)/(7)=90`

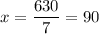
Therefore, there are 3x = 3*(90) = 270 longs

Answer: there are 270 longs