Question

A class has an equal number of boys and girls. The boys all got 78% on a test and the girls all got 84%. What are the mean and standard deviation of the test scores for the entire class?

Answer 1

Mean is 81%

standard deviation is approximately 4.2%

Explanation:

Since the number of boys equals the number of girls, but it is not given, we name it "N". and proceed to calculate the mean as:

Mean = (0.78 * N + 0.84 * N) /(2 N)

using that the total number of students must be N boys + N girls = 2 N

Then the Mean becomes: N *(0.78 + 0.84) /(2 N) = (0.78 + 0.84) / 2 = 1.62 / 2 = 0.81

So the mean is 81%

Now, standard deviation will be calculated by first adding the squares of the deviations: (X-0.81)^2 for the N boys and for the N girls, and then finding the square root of this and finally dividing by the square root of N. That is:

`N\,(0.78-0.81)^2\,+\,N\,(0.84-0.81)^2= N \left \{ (-0.03)^2+(0/03)^2\right \}=N\,*0.0018`

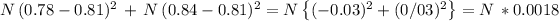
Now finding the square root of this value, and finally dividing it by the square root of N:

`\sigma=(√(N\,*\,0.0018) )/(√(N) ) =√(0.0018) \approx 0.042426`

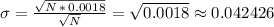
which in percent form is: approximately 4.2%