Question

Find all the points (-105,y) that are 17 units from the point P (-97,2)

Answer 1

The points that are 17 units from P(-97,2) are:

(-105,-13) and (-105,17)

Explanation:

Distance between two points

The distance between points A(x,y) B(w,z) can be calculated with the formula:

`d=√((w-x)^2+(z-y)^2)`

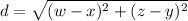
One point is (-105,y) and the other is (-97,2). Computing the distance between them:

`d=√((-97-(-105))^2+(2-y)^2)=√(8^2+(2-y)^2)=√(64+(2-y)^2)`

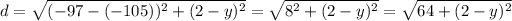
This distance is 17, thus:

`√(64+(2-y)^2)=17`

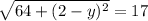
Squaring on both sides:

`64+(2-y)^2=289`

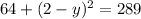
Operating:

`(2-y)^2=289-64=225`

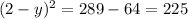
Taking the square root:

`(2-y)=\pm 15`

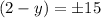
There are two possible solutions:

`2-y=15\Rightarrow y=-13`

`2-y=-15\Rightarrow y=17`

The points that are 17 units from P(-97,2) are:

(-105,-13) and (-105,17)