Question

The shorter leg of a right triangle is 7 ft shorter than the longer leg. The hypotenuse is 7 ft longer than the longer leg. Find the side lengths of the triangle.​

Answer 1

shorter leg = 21 ft

longer leg = 28 ft

hypotenuse = 35 ft

Explanation:

Let's call the longer leg of the triangle "b", the shorter leg "a", and the hypotenuse "h"

Then we have the following two equations:

a = b - 7

h = b + 7

And we can use the Pythagorean theorem to relate all three sides of the triangle:

`h^2=a^2+b^2\\(b+7)^2=(b-7)^2+b^2\\b^2+14b +49=b^2-14b+49+b^2\\0=b^2-28b\\0=b*(b-28)`

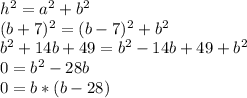
Therefore there are two possible solutions to this equation: b = 0 or b = 28 ft.

So we take the one that is different from zero (since we are looking for the side of a triangle) That is: b = 28 ft

Then hypotenuse = 28 + 7 = 35 ft

and the shorter leg = 28 - 7 = 21 ft